Statistical & Financial Consulting by Stanford PhD
Home Page
KENDALL'S TAU
 = \textrm{P}\bigl((X_1 - X_2)(Y_1 - Y_2) > 0\bigr) - \textrm{P}\bigl((X_1 - X_2)(Y_1 - Y_2) < 0\bigr).\ \ \ \ \ \ \ \textbf{(1)})
If
and
have continuous marginal distributions then
 )
has the same units as Pearson's correlation. Just like Pearson's correlation it covers the whole range of [-1,1], but now -1 corresponds to a perfect negative relationship (
is any decreasing deterministic function of ) and 1 corresponds to a perfect positive relationship ( is any increasing deterministic function of ). When
or
has a discrete mass, interval [-1,1] is not covered fully. For example, if variable
takes a given value with positive probability p, then with probability of at least p2 there is a tie:
And so
falls into interval [-1 + p2, 1 - p2]
no matter what the bivariate relationship is. There are several proposals on how to adjust for ties, the most obvious one being to divide formula (1) by
(Y_1 - Y_2) = 0\bigr).)
Still, no single generalization has been widely accepted.
Note that definition (1) depends on ranks only. We only care if
is bigger than
the actual values being irrelevant. So Kendall's tau is invariant to any monotonically increasing nonlinear transformations of
and 
If we raise
to the third power Kendall's tau will stay the same. This is very important. Kendall's tau is naturally built to capture the strength of highly nonlinear relationships, where traditional linear association measures fail. The following graph illustrates the fact.
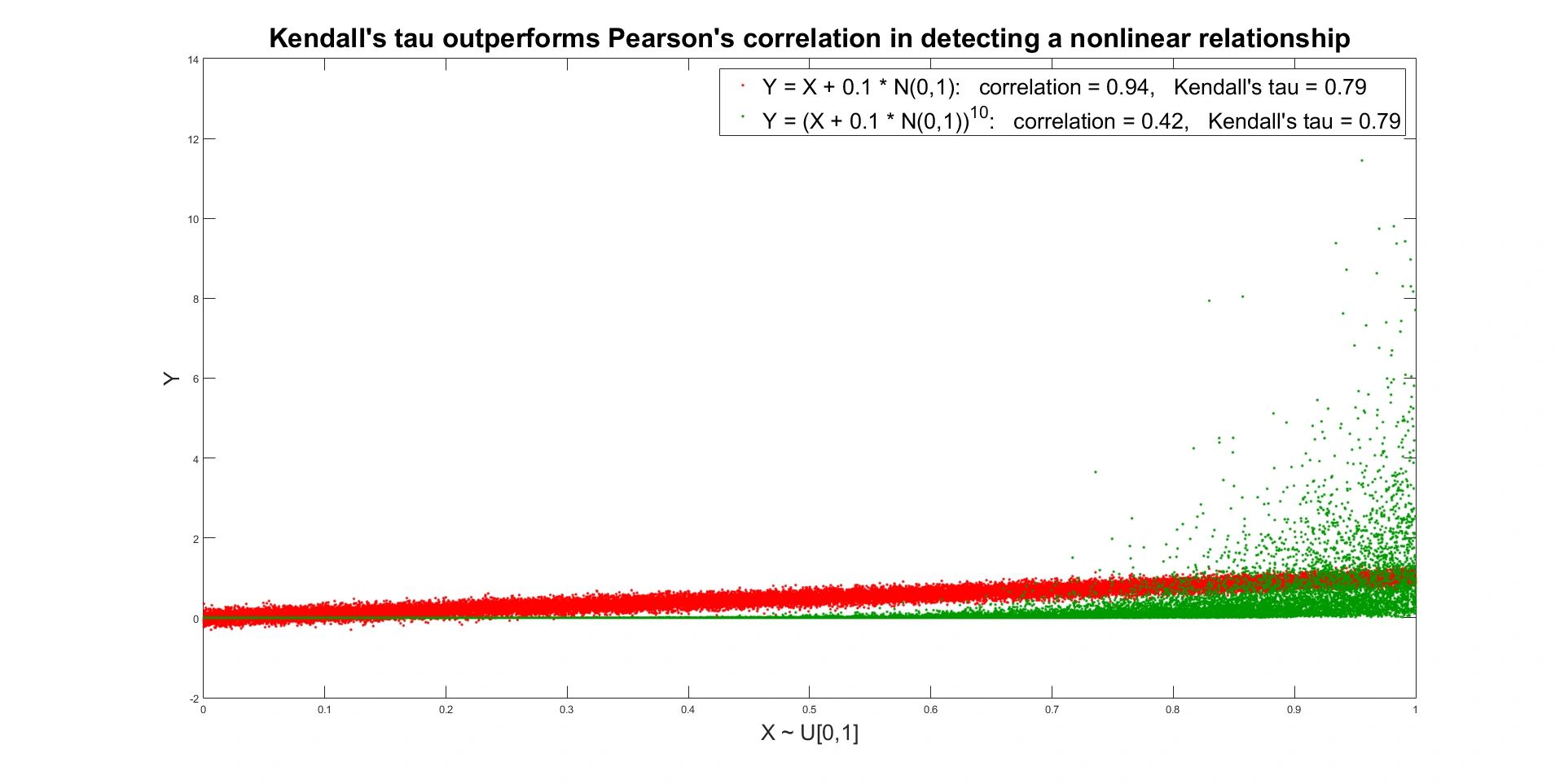
Kendall's tau has direct relation to the copula function)
generated by random variables
and
 = 4 \int\int_{[0,1]^2} C(u,v)\ dC(u,v) - 1.)
The copula function does not depend on marginal distributions and captures what happens to
and
if they are transformed into random variables uniformly distributed on [0,1]. The formula above signals once again that Kendall's tau does not depend on marginal distributions of
and
and is invariant to any monotonically increasing transformations of
and
Several sample estimators have been developed. Let, ..., (X_n,Y_n))
denote observations from the joint distribution of
and
Pairs
)
and
)
are called
concordant if their ranks agree:
or
discordant if their ranks disagree:
or
tied if
or
Let
number of concordant pairs,
number of discordant pairs,
number of unique values in
number of unique values in
number of tied values in the i-th group of ties in
number of tied values in the j-th group of ties in
}{2},)
}{2},)
}{2}.)
The estimators of
are defined as
(N-N_Y)}},)
}{(q-1)n^2}.)
Estimators
and
make adjustments for ties and are suitable for all distributions.
Estimator
does not adjust for ties and is suitable only for continuous distributions measured with high precision.
Each of the estimators
is nonparametric in the sense that it makes little or no assumptions about the joint distribution of
and
In particular, no functional form is postulated for the conditional expectation of
given
and the conditional expectation of
given
For each of the estimators
tests have been developed, telling us if
equals 0. A typical test is based on a transformation of the estimator which is asymptotically normal (its distribution converges to a normal distribution when the sample size grows big).
KENDALL'S TAU REFERENCES
Nelsen, R. B. (2006). An Introduction to Copulas (2nd ed). New York: Springer.
Salvadori, G., De Michele, C., Kottegoda, N. T., & Rosso, R. (2007). Extremes in Nature: An Approach Using Copulas. Springer.
Gibbons, J. D., & Chakraborti, S. (2003). Nonparametric Statistical Inference (4th ed). New York: Marcel Dekker.
Nešlehová, J. (2007). On Rank Correlation Measures for Non-continuous Random Variables. Journal of Multivariate Analysis, Vol. 98, Issue 3, pp. 544-567.
Kendall, M. (1938). A New Measure of Rank Correlation. Biometrika, Vol. 30 (1–2), pp. 81–89.
BACK TO THE STATISTICAL ANALYSES DIRECTORY
IMPORTANT LINKS ON THIS SITE
Kendall's Tau (Kendall's Rank Correlation Coefficient) is a measure of nonlinear dependence between two random variables. If random variables
and
have joint distribution
and random vectors
and
are independent realizations from that distribution, then Kendall's tau of
and
equals
If
Still, no single generalization has been widely accepted.
Note that definition (1) depends on ranks only. We only care if
Kendall's tau has direct relation to the copula function
The copula function does not depend on marginal distributions and captures what happens to
Several sample estimators have been developed. Let
concordant if their ranks agree:
discordant if their ranks disagree:
tied if
Let
The estimators of
Estimators
KENDALL'S TAU REFERENCES
Nelsen, R. B. (2006). An Introduction to Copulas (2nd ed). New York: Springer.
Salvadori, G., De Michele, C., Kottegoda, N. T., & Rosso, R. (2007). Extremes in Nature: An Approach Using Copulas. Springer.
Gibbons, J. D., & Chakraborti, S. (2003). Nonparametric Statistical Inference (4th ed). New York: Marcel Dekker.
Nešlehová, J. (2007). On Rank Correlation Measures for Non-continuous Random Variables. Journal of Multivariate Analysis, Vol. 98, Issue 3, pp. 544-567.
Kendall, M. (1938). A New Measure of Rank Correlation. Biometrika, Vol. 30 (1–2), pp. 81–89.
BACK TO THE STATISTICAL ANALYSES DIRECTORY
IMPORTANT LINKS ON THIS SITE
- Detailed description of the services offered in the areas of statistical and financial consulting: home page, types of service, experience, case studies, payment options and actuarial science tutoring
- Directory of financial topics